今回は電気回路の交流回路で使用されるインピーダンスについて解説していきます。
インピーダンスとは
インピーダンスとは交流回路における抵抗の役割を果たすものです。
一般的に\(Z=R+jX\)と表されます。
それぞれ、説明すると
Z:インピーダンスで単位は抵抗と同じΩを使用します。
R:直流と同じ抵抗を表します。
X:リアクタンスといい、ここが交流の抵抗値を表します。
j:これは虚数単位で数学ではiが使われています。しかし、電気回路では電流をiで表すので、jが使われています。
インピーダンスは抵抗と同じく合成抵抗は
\(Z=Z_1+Z_2+Z_3+…\)で求めることができます。
インピーダンスはさまざまな要因によって発生しますが、今回は良くよく使われ、出てくるコイルとコンデンサのインピーダンスについて説明していきます。
コイルのインピーダンス
コイルのインピーダンスは\(Z_L=jωL\)で表されます。
\(ω\):角周波数で\(ω=2πf\)なので\(Z_L=j2πfL\)と表すこともできます。
コイルでは周波数が小さい場合は、抵抗のように小さい負荷を生みますが、周波数が大きい場合はインピーダンスが無限に近づくので開放の状態となります。
コンデンサのインピーダンス
コンデンサのインピーダンス\(Z_C=\frac{1}{jωC}=\frac{1}{j2πfC}\)で表されます。
コンデンサは周波数が小さい場合に開放状態となり、周波数が小さい場合は短絡状態になります。
つぎにコイルとコンデンサを使った回路の合成インピーダンスを求めていきます。
問題1

この回路の合成インピーダンスは
\(Z=R+jωL\)
問題2

この回路の合成インピーダンスは
\(Z=R+\frac{1}{jωC}\)
問題3

この回路の合成インピーダンスは
\(Z=R+jωL+\frac{1}{jωC}\)
問題4
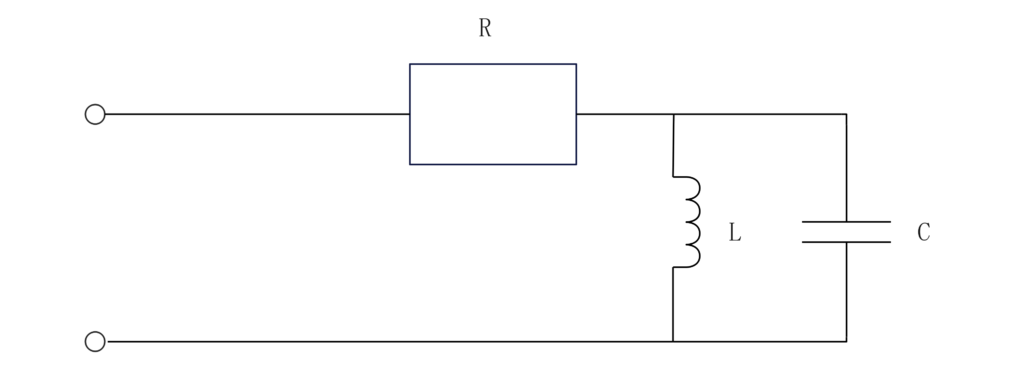
この回路の合成インピーダンスは
\(Z=R+jωL//\frac{1}{jωC}\)
ここで、\(Y_{LC}=\frac{1}{jωL}+jωC=\frac{1}{jωL}+\frac{jωL・jωC}{jωL}=\frac{1-ω^2LC}{jωL}\)
よって、\(Z=R+\frac{1}{Y_{LC}}=R+\frac{jωL}{1-ω^2LC}\)となります。
問題5
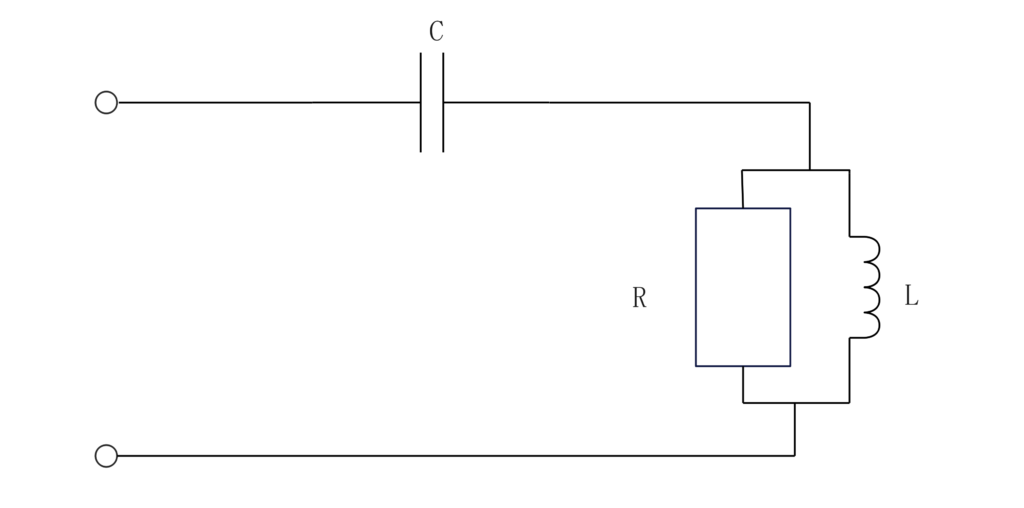
この回路の合成インピーダンスは
\(Z=\frac{1}{jωC}+R//jωL=\frac{1}{jωC}+\frac{jωLR}{R+jωL}\)
この後にこの式を通分にして一つの式にまとめてもいいですが余計に複雑になるのでここで止めておく方がいいです。
それでも計算したい場合答えは\(Z=\frac{ω^2LCR-j(R+ωL)}{ωC(ωL-jR)}\)となります。
このように交流回路の合成インピーダンスは直流回路の抵抗を求めるときと同じように計算することができます。



コメント