合成抵抗の求め方

抵抗を接続する方法には直列接続、並列接続、直並列接続の3種類があります。

今回はそれぞれの接続方法による回路の合成抵抗を求めていきます。

直列接続と並列接続の違い

直列接続

直列接続・・・電流はどこの場所でも常に一定、電圧は抵抗の値によって変化する。

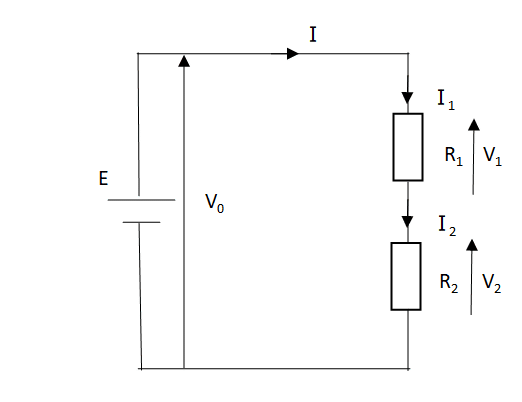
上の回路の場合、V₀=V₁+V₂、 I₀=I₁=I₂

並列接続

並列接続・・・電流は抵抗の値によって変化、電圧は常に一定である。

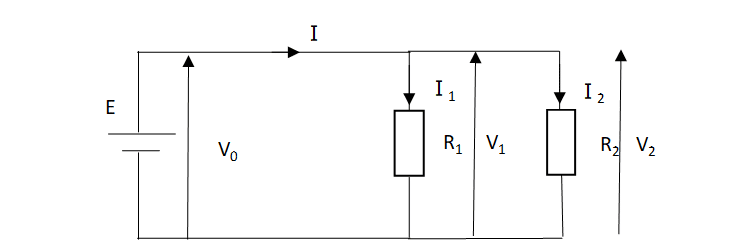
上の回路の場合、I₀=I₁+I₂ 、V₀=V₁=V₂

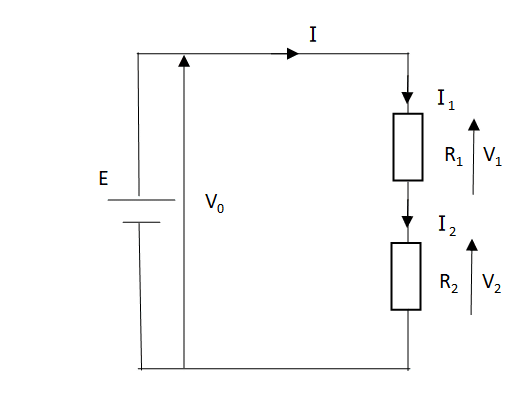
直列回路

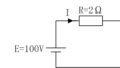
直列回路は以下の図のような回路のことです。

直列接続の電流はどこの場所でも常に一定であるため

オームの法則より電圧Ｖ₀=I・R₀(R₀:合成抵抗)・・・(1-1)
Ｖ₁=I・R₁ 、V₂=I・R₂ がわかる。
V₀=V₁+V₂より、V₀= I・R₁+ I・R₂=Ⅰ(R₁+R₂)・・・(1-2)
(1-1)、(1-2)より　I・R₀=Ⅰ(R₁+R₂)
R₀= R₁+R₂
以上により、２つの直列接続の合成抵抗はR₀= R₁+R₂で求められることがわかる

３つ以上の場合

3つ以上の場合も同様にして解くと、R₀=R1+R2+・・・＋Rnで求められることがわかる

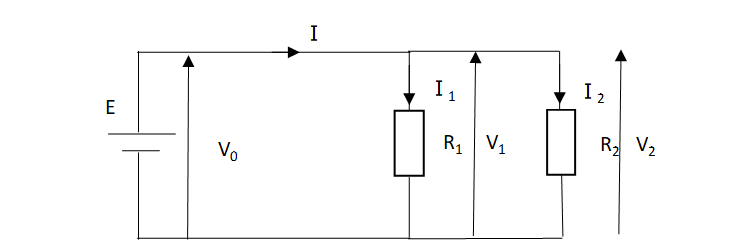
並列回路

並列接続は以下の図のような回路のことです。

並列接続の電圧は常に一定であるため

オームの法則より、$${I_0=\frac{V}{R_0}…(2-1)}$$
$${ I_1=\frac{V}{R_1}}$$ $${ I_2=\frac{V}{R_2}}$$
\(I_0=I_1+I_2\)より、$${I_0=\frac{V}{R_1}+\frac{V}{R_2}=\frac{R_1＋R_2}{ R_1・R_2}・V…(2-2)}$$
(2-1)を(2-2)に代入すると、$${\frac{V}{R_0}=\frac{R_1＋R_2}{ R_1・R_2}・V}$$
　　　　　　　$${\frac{1}{R_0}=\frac{R_1＋R_2}{ R_1・R_2}}$$
　　　　　　　$${ R_0=\frac{R_1・R_2}{ R_1＋R_2}}$$
ここで、右辺の分母分子を\(R_1・R_2\)で割ると、
　　　　　　$${ R_0=\frac{1}{\frac{1}{R_1}＋\frac{1}{R_2}}}$$
以上により、２つの並列接続の合成抵抗は$${ R_0=\frac{R_1・R_2}{ R_1＋R_2}}$$で求められる

３つ以上の場合

３つ以上の場合も同様にして解くと、
$${ R_0=\frac{1}{\frac{1}{R_1}＋\frac{1}{R_2}+・・・+\frac{1}{Rn}}}$$　 　　　　　　　　 で求められる

直並列回路

直並列接続とは直列接続と並列接続が合わさったもので、以下のような図のことです。

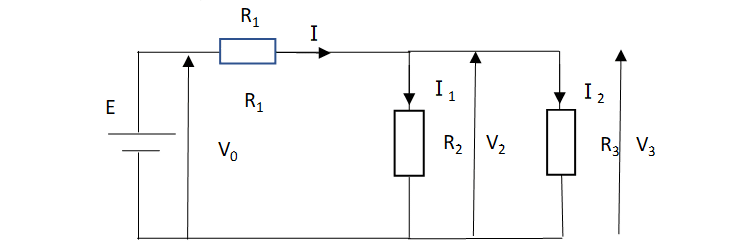
直並列回路の合成抵抗を解くときのこつ

1. 並列接続の合成抵抗を求め、一つの抵抗とみなす
2. 直並列回路から直列回路に直し抵抗をすべて足し、全体の合成抵抗を求める。

実際に上の図について解いてみると
１　並列接続の合成抵抗は

$${R_{23}=\frac{R_2・R_3}{R_2＋R_3}}$$

＊R₂₃：R₂とR₃の合成抵抗
で求められる。

2　直列回路に直すと以下の図になり、

合成抵抗R₀は

$${R_0=R_1+R_{23}=R_1+\frac{R_2・R_3}{R_2＋R_3}}$$

で求められる。

コンダクタンスによる合成抵抗の求め方

抵抗R[Ω]の逆数をコンダクタンスといい、G[S]で表現します。　*S:ジーメンス

コンダクタンス、抵抗、電流、電圧の関係

                                    $${G=\frac{1}{R}=[S]}$$
                                    $${G=\frac{Ｉ}{V_0}=[S]}$$

下の並列回路に対して、コンダクタンスを使用して合成回路を求めていきます。

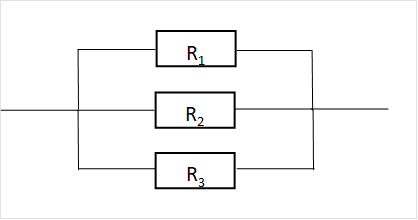
$${R_0=\frac{1}{\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}}}$$

$${G=\frac{1}{R}}$$より
$${\frac{1}{G_0}=\frac{1}{G_1+G_2+G_3}}$$
G₀＝G₁+G₂+G₃

例題

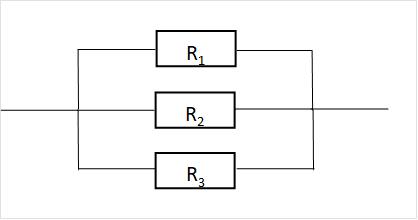
R1=100[Ω] , R2=200[Ω] , R3=300[Ω]とします。

コンダクタンスを使用する場合

$${G_0＝\frac{1}{100}+\frac{1}{200}+\frac{1}{300}=\frac{11}{600}}$$
$${R_0=\frac{1}{G_0}=\frac{600}{11}}$$

コンダクタンスを使用しない場合

$${R_0=\frac{1}{\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}}=\frac{600}{11}}$$

以上によりコンダクタンスを求めることにより合成抵抗が求められることがわかる。

結論

回路の合成抵抗を求めるときは
直列接続…R₀=R₁+R₂+…＋R_n
並列接続…$${R_0=\frac{1}{\frac{1}{R_1}+\frac{1}{R_2}+…\frac{1}{Rn}}}$$

コンダクタンス${G=\frac{1}{R}}$を応用することで機械的に合成抵抗を求めることができるようになります。