T型抵抗減衰器は信号の振幅を一定量減衰させるために用いられます。用途としては高周波回路、通信機器などで、不要な強度を抑え指定したインピーダンス整合を行うために利用されます。
概要

T型抵抗減衰器はこの回路のようにT型形状に抵抗を配置した減衰回路で、出力を入力に関わらず入力に信号に対して特定の減衰量を与え、選択したインピーダンスで整合を取ることができます。
一般的に高周波の伝送では標準的な特性インピーダンスとして50Ωが採用されています。これは伝送特性のバランスが良好なためこの値が使用されています。
そのため今回は特性インピーダンスを50Ωとして解説していきます。
※特性インピーダンスが50Ω以外でも適応することができます。
R1、R2の導出

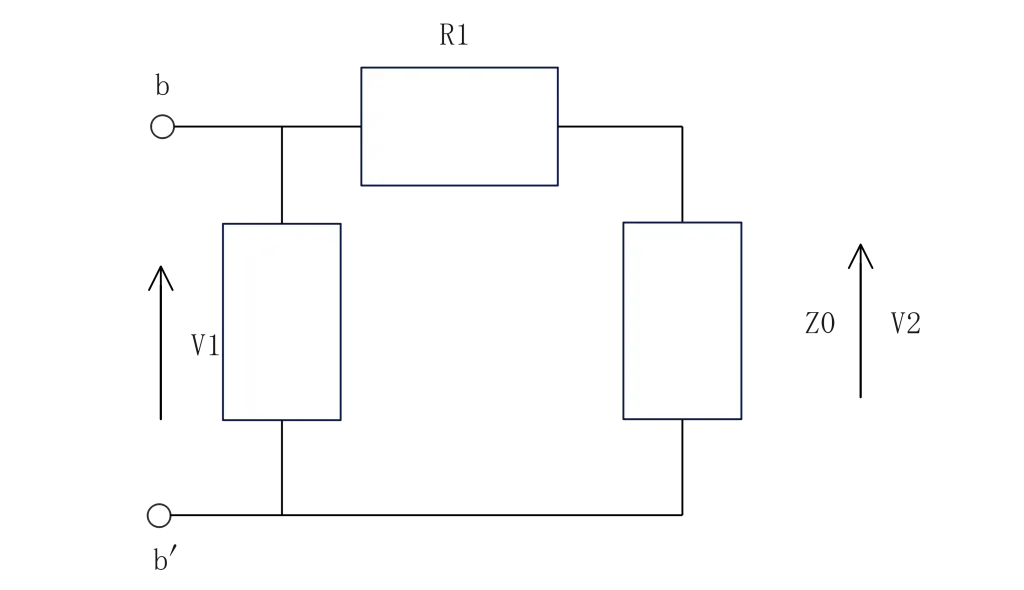
まずこのような回路を考えます。
ここで特性インピーダンスは50ΩなのでZ0=50とします。
この回路で整合を取るには回路のインピーダンスと特性インピーダンスを等しくしないといけないので、a-a’間の入力インピーダンスを求めます。
入力インピーダンスをZiとすると
\(Zi=R_1+\frac{R_2(R_1+Z_0}{R_2+(R_1+Z_0)}\)
ここでb-b’間の合成抵抗をZ2とすると
\(Z_2=\frac{R_2(R_1+Z_0}{R_2+(R_1+Z_0)}\)
ここでa-a’間の電圧をV1、b-b’間の電圧をV3、負荷のインピーダンスZ0にかかる電圧をV2とすると、

V1とV3の関係は
\(V_3=\frac{Z_2}{R_1+Z_2}V_1\)
V2とV3の関係は
\(V_2=\frac{Z_0}{R_1+Z_0}V3\)=\(
\frac{Z_0}{R_1 + Z_0} \cdot \frac{Z_2}{R_1 + Z_2} =
\frac{Z_0}{R_1 + Z_0} \cdot
\frac{\frac{R_2 (R_1 + Z_0)}{R_2 + (R_1 + Z_0)}}{R_1 + \frac{R_2 (R_1 + Z_0)}{R_2 + (R_1 + Z_0)}} V_1
\)
ここで、整合がとれている場合回路のインピーダンスと特性インピーダンスを等しくなるためZi=Z0となります。
これより、\(V_2=\frac{Z_0}{R_1+Z_0}・\frac{\frac{R_2(R_1+Z_0)}{R_2+(R_1+Z_0)}}{Z_0}V_1=\frac{R_2}{R_2+(R_1+Z_0)}V_1\)
ここで、電圧減衰比Kには\(K=\frac{V_1}{V_2}\)の関係があります。
また、電圧減衰率は\(G=20log_{10}K\)。
\(K=\frac{V_1}{V_2}=\frac{R_2+(R_1+Z_0)}{R_2}\)・・・(1)
ここで入力インピーダンスZiと特性インピーダンスZ0が等しいため
\(Zi=R_1+\frac{R_2(R_1+Z_0}{R_2+(R_1+Z_0)}\)
ここに式(1)を代入すると
\(Zi=R_1+\frac{R_1+Z_0}{K}=Z_0\)
\(KR_1+R_1=KZ_0-Z_0\)
\(R_1(K+1)=Z_0(K-1)\)
\(R_1=Z_0\frac{K-1}{K+1}\)
式(1)よりR2について解くと
\(R_2K=R_2+R_1+Z_0\)
\(R_2(K-1)=R_1+Z_0\)
\( R_2 = \frac{ \frac{ \frac{K-1}{K+1} Z_0 + Z_0 }{ K-1 } }{ \frac{K-1}{K-1} } = \frac{2K}{K^2 – 1} Z_0 \)
電圧減衰率を6dB、特性インピーダンスを50Ωとすると、
\(6=20log_{10}K\)
\(10^\frac{6}{20}\simeq1.995\)
これを代入すると、
\(R_1=50\frac{K-1}{K+1}\simeq16.61[Ω]\)
\(R_2=50\frac{2K}{K^2-1}\simeq66.93[Ω]\)
これで整合条件であるR1とR2が求まりました。


コメント