今回は抵抗とコンデンサを組み合わせたRC直列回路について説明していきます。
RC直列回路は発振回路や微分・積分回路などに使われています。
RC直列回路
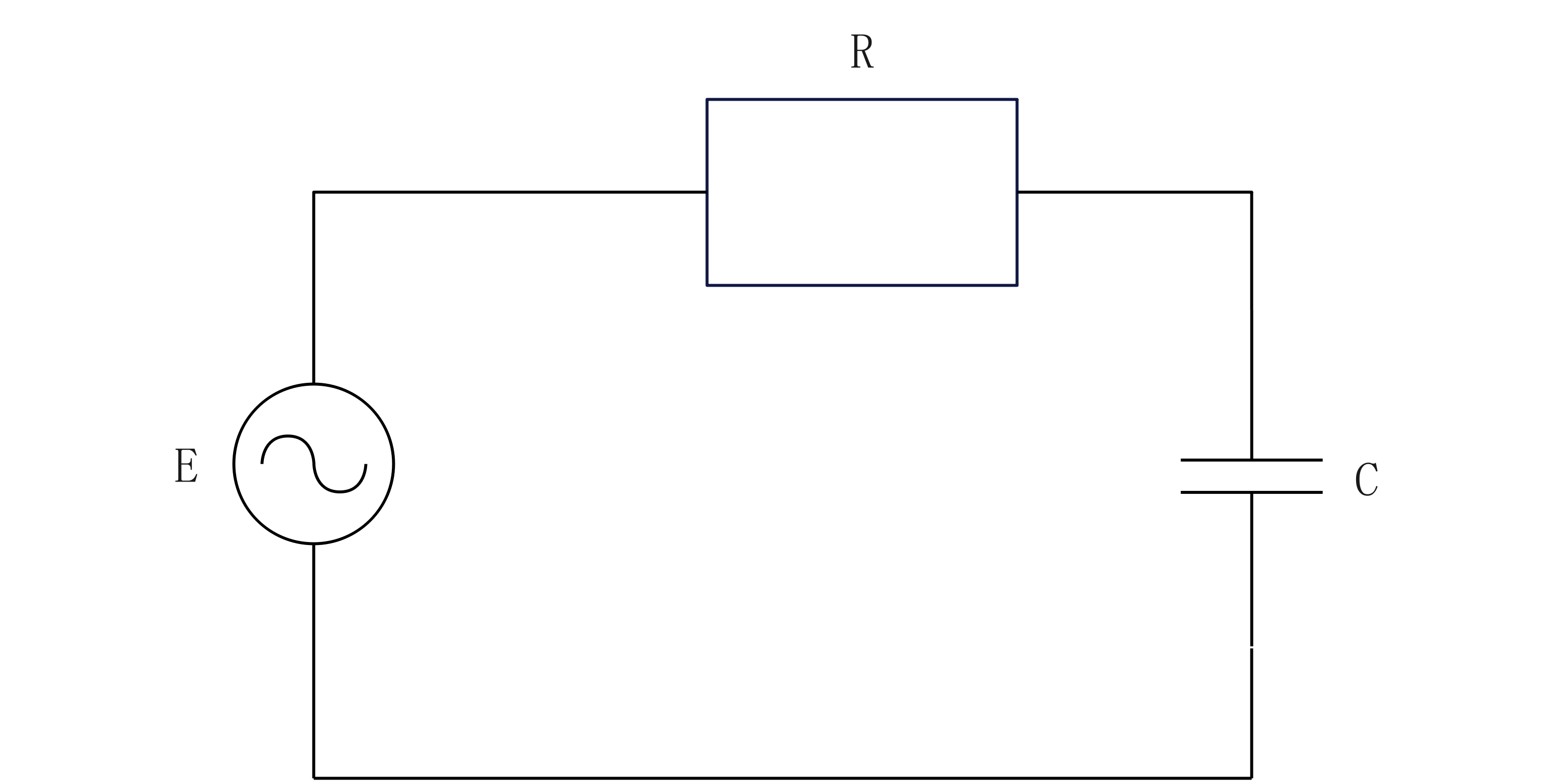
下のような回路をRC直列回路といいます。
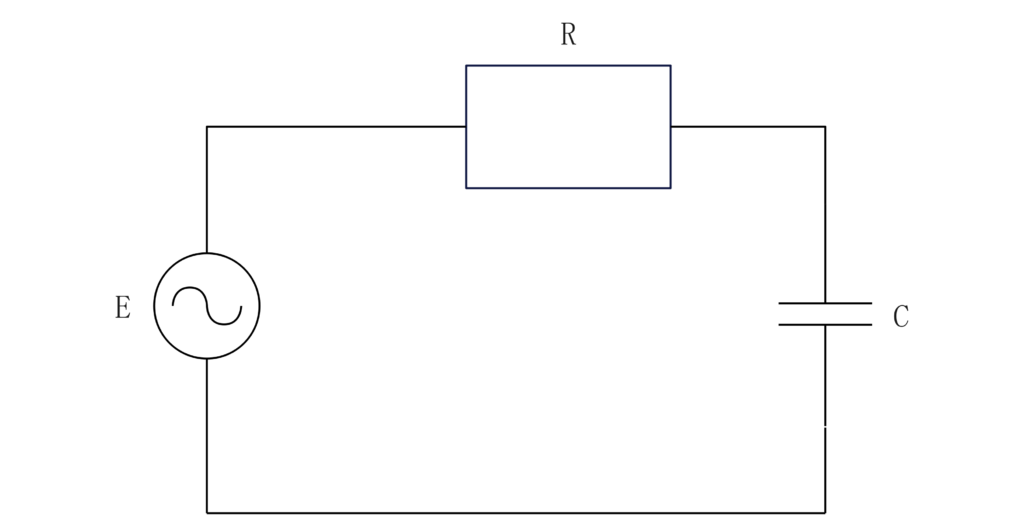
この回路に電源を供給すると、抵抗とコンデンサに電圧がかかります。
この回路の合成インピーダンスは\(Z=R+\frac{1}{jωC}\)
合成電圧は\(E(t)=Ri(t)+\frac{i(t)}{jωC}\)となります。
コンデンサは電圧をかけると充電され、充電されるにつれ流れる電流が小さくなり、充電が100%になると電流は流れなくなります。
この電圧と電流の時間関係は次にような式になります。
ます、抵抗RとコンデンサCにかかる電圧はそれぞれ
\(v_R=Ri(t)\)
\(v_C=\frac{q}{C}\) q:静電容量
\(i=\frac{dq}{dt}\)
より\(E=v_R+v_C=R\frac{dq}{dt}+\frac{q}{C}\)
ここで特解を求めるために定常である電源Eを除去して計算します。
\(R\frac{dq}{dt}=-\frac{q}{C}\)
\(\frac{1}{q}dq=-\frac{1}{RC}dt\)
\(log|q|-\frac{1}{RC}t+C\)
\(q=e^{-\frac{1}{RC}t+C}\)
\(A=e^C\)と置くと
\(q=Ae^{-\frac{1}{RC}t}\)
次に一般解を求めるために定常状態の電圧を考えると、\(\frac{dq}{dt}=0\)となるので\(q=CE\)
この解を一般解と合わせると
\(q(t)=Ae^{\frac{1}{RC}t}+CE\)
初期条件より\(t=0\)のとき\(q(t)=0\)なので
\(A=-CE\)
よって、\(q(t)=CE(1-e^{-\frac{1}{RC}t})\)
また、\(i(t)=\frac{dq(t)}{dt}=\frac{EC}{RC}e^{-\frac{1}{RC}t}=\frac{E}{R}e^{-\frac{1}{RC}t}\)
\(V_R=Ri(t)=Ee^{-\frac{1}{RC}t}\)
\(V_C=\frac{q(t)}{C}=E(1-e^{-\frac{1}{RC}t})\)


コメント