今回は抵抗とインダクタを組み合わせたRL回路について説明していきます。
RL回路は周波数制限を行うフィルタ回路などに使われています。
RL直列回路
下のような回路をRL直列回路といいます。
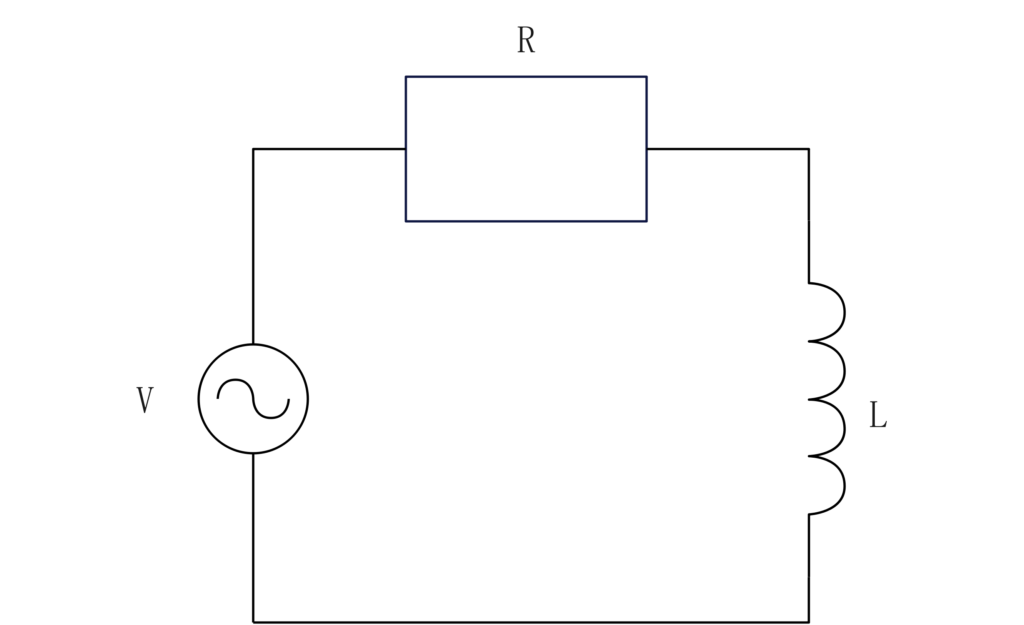
この回路に電源を供給すると、抵抗とインダクタに電圧がかかります。
この回路の合成インピーダンスは\(Z=R+iωL\)
合成電圧は\(V(t)=Ri(t)+jωLi(t)\)となります。
しかし、インダクタにかかる電圧はすぐに最大値にならず少しずつ大きくなります。
まず、抵抗RとインダクタLにかかる電圧はそれぞれ
\(v_R=Ri\)
\(v_L=L\frac{d(i)}{dt}\)
\(V=v_R+v_L=Ri+L\frac{d(i)}{dt}\)となります。
ここで、iを求めるため式を変形すると
\(\frac{d(i)}{dt}+\frac{R}{L}i=\frac{V}{L}\)
ここで、\(\frac{V}{L}\)は定常であり、電流の変化に関与しないため、特解を求めるために右辺を除去します。
すると、
\(\frac{di(t)}{dt}=-\frac{R}{L}i(t)\)
\(\frac{1}{i(t)}\frac{di(t)}{dt}=-\frac{R}{L}\)
ここで、tについて積分すると
\(\int \frac{1}{i(t)}di(t)=-\frac{R}{L}\int dt\)
\(log|i(t)|={-\frac{R}{L}t}+C\)
\(i(t)=e^{-\frac{R}{L}t}+C\) \(e^C=A\)と置くと
\(i(t)=Ae^{-\frac{R}{L}t}\)
次に一般解を求めるために定常状態の電流を考えると、\(\frac{di}{dt}=0\)(時間による変化がないため)となるので、\(I_{t=∞}=\frac{V}{R}\)となります。
この解を特解と合わせると、
\(i(t)=L\frac{Ae^{-\frac{R}{L}t}}{dt}+\frac{V}{R}=Ae^{-\frac{R}{L}t}+\frac{V}{R}\)
となります。
そして、初期条件よりt=0のとき(つまりスイッチを入れた瞬間は電流が0なので)、I=0より
\(0=Ae^0+\frac{V}{R}\)より
\(A=-\frac{V}{R}\)
よって、
\(i(t)=-\frac{V}{R}e^{-\frac{R}{L}t}+\frac{V}{R}=\frac{V}{R}(1-e^{-\frac{R}{L}t})\)
それぞれ、抵抗にかかる電圧\(V_R(t)\)、\(V_L(t)\)を求めると、
\(V_R(t)=RI(t)=V(1-e^{-\frac{R}{L}t})\)
\(V_L(t)=L\frac{di(t)}{dt}=L\frac{\frac{V}{R}-\frac{V}{R}e^{-\frac{R}{L}t}}{dt}=Ve^{-\frac{R}{L}}\)

コメント