今回はキルヒホッフの法則の演習問題を解いていきます。
自分で解ける人は最初に自分で解いてから回答を見てください。
問題1
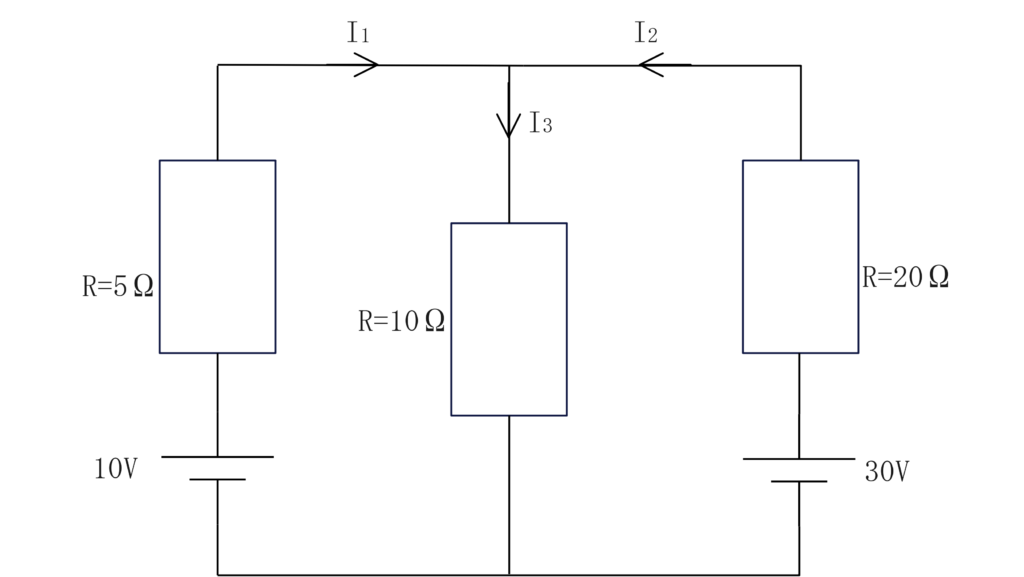
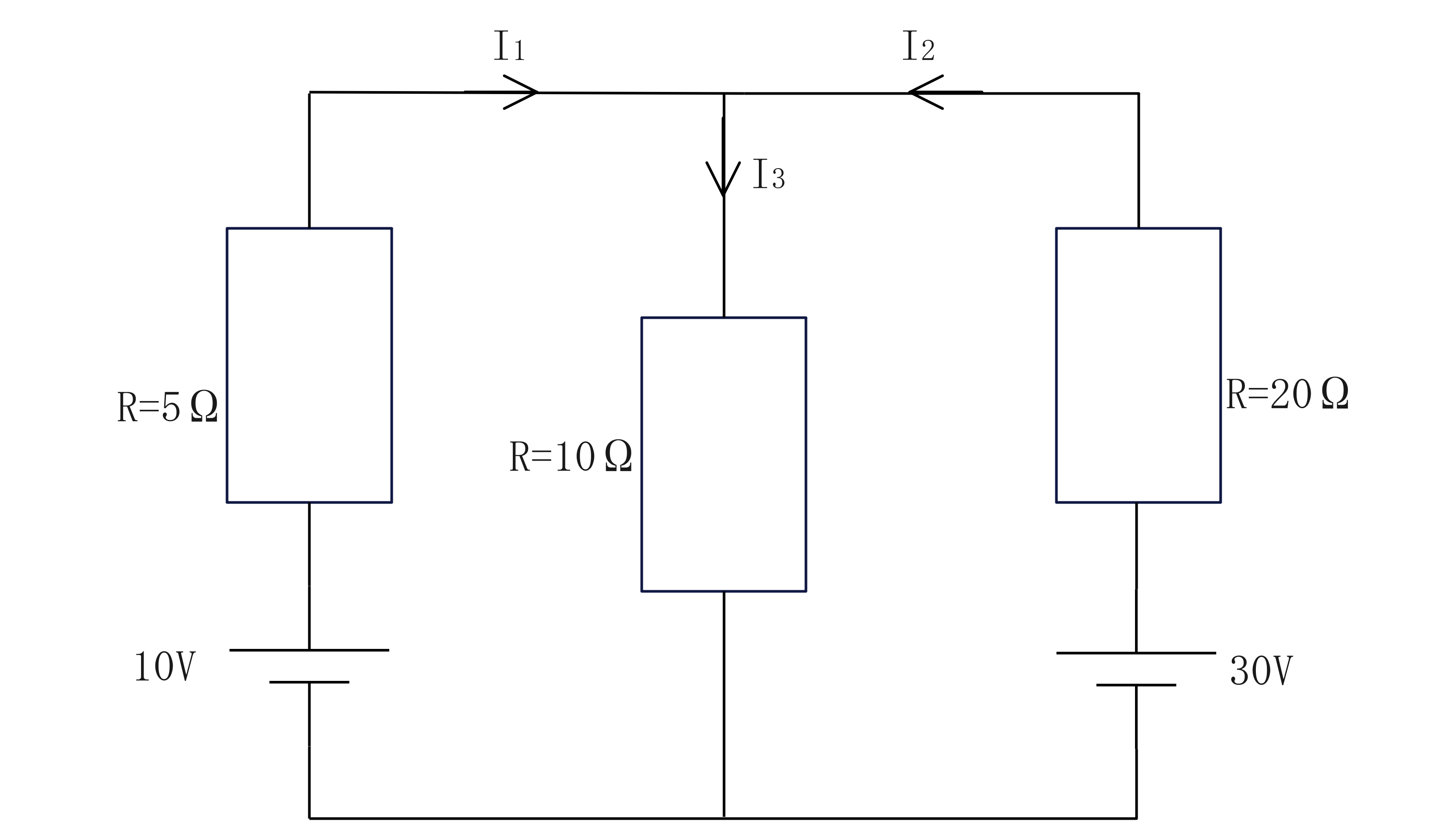
以下の回路で\(I_1、I_2、I_3\)について解きなさい。
まず連立方程式を作成します。
左の閉回路より\(10=5I_1+10I_3…①\)
右の閉回路より\(30=20I_2+10I_3…②\)
キルヒホッフの第一法則より\(I_1+I_2=I_3…③\)
③より\(I_2=I_3-I_1\)となります。
これを②に代入すると
\(30=20(I_3-I_1)+10I_3…④\)となります。
①×4+④より
\(40=20I_1+40I_3\)
\(30=-20I_1+30I_3\)
\(70=I_3\)
よって\(I_3=1[A]\)となります。
これを①に代入すると\(I_1=0[A]\)
③に代入すると\(I_2=1[A]\)となります。
問題2
以下の回路で\(I_1、I_2、I_3\)について解きなさい。
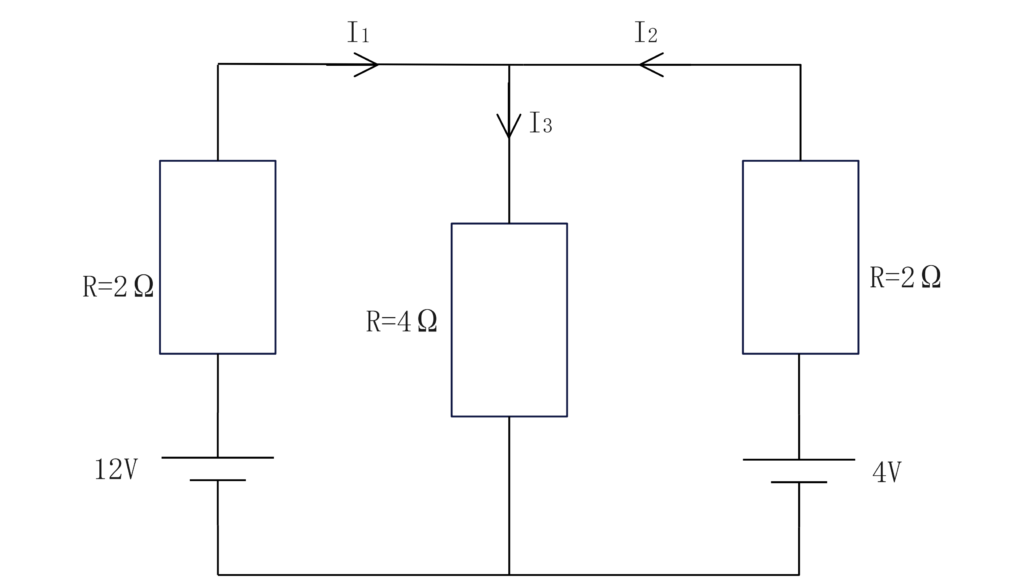
\(12=2・I_1+4・I_3…①\)
\(4=2・I_2+4・I_3…②\)
\(I_1+I_2=I_3…③\)
➀、②に➂を代入すると
\(12=6・I_1+4・I_2…④\)
\(4=4・I_1+6・I_2…⑤\)
④×2-⑤×3より
\(24=12I_1+8I_2\)
\(12=12I_1+18I_2\)
\(12=-10I_2\)
\(I_2=-\frac{6}{5}[A]\)
これを④に代入すると
\(12=6I_1-\frac{24}{5}\)
\(6I_1=12+\frac{24}{5}\)
\(I_1=2+\frac{4}{5}=\frac{14}{5}[A]\)
③より
\(I_3=\frac{14}{5}-\frac{6}{5}[A]\)
問題3
以下の回路で\(I_1、I_2、I_3\)について解きなさい。
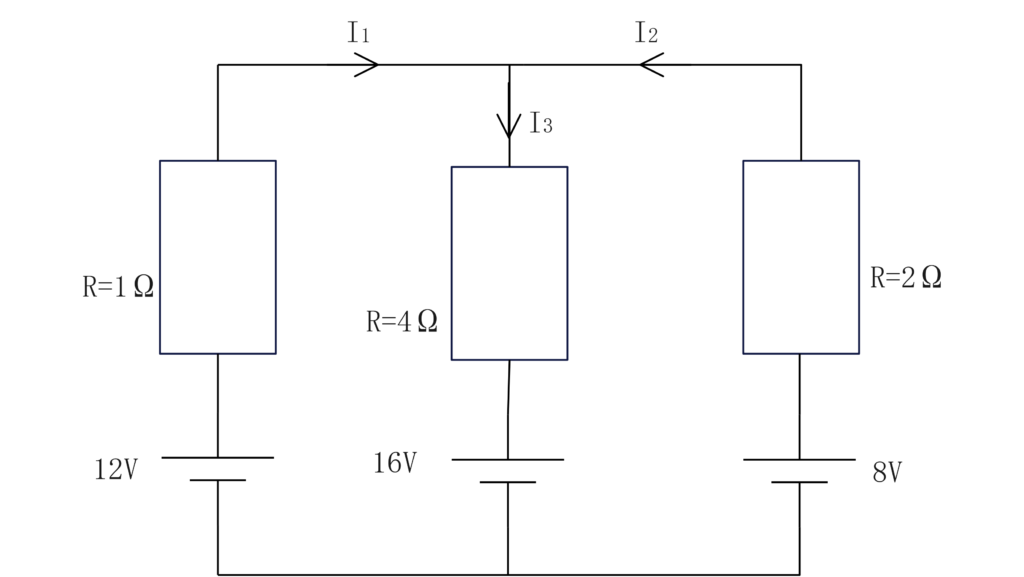
\(12-16=I_1+4I_3…①\)
\(8-16=2I_2+4I_3…②\)
\(I_1+I_2=I_3…③\)
③を➀、②に代入すると
\(-4=I_1+4(I_1+I_2)\)
\(-8=2I_2+4(I_1+I_2)\)
これを展開すると
\(-4=5I_1+4I_2…④\)
\(-8=4I_1+6I_2…⑤\)
④×3-⑤×2より
\(-12=15I_1+12I_2\)
\(-16=8I_1+12I_2\)
\(7I_1=4\)
\(I_1=\frac{4}{7}[A]\)
これを④に代入すると
\(-4=5・\frac{4}{7}+4I_2\)
\(4I_2=-4-\frac{20}{7}\)
\(I_2=-1-\frac{5}{7}=-\frac{12}{7}[A]\)
③より
\(\frac{4}{7}-\frac{12}{7}[A]\)
問題4
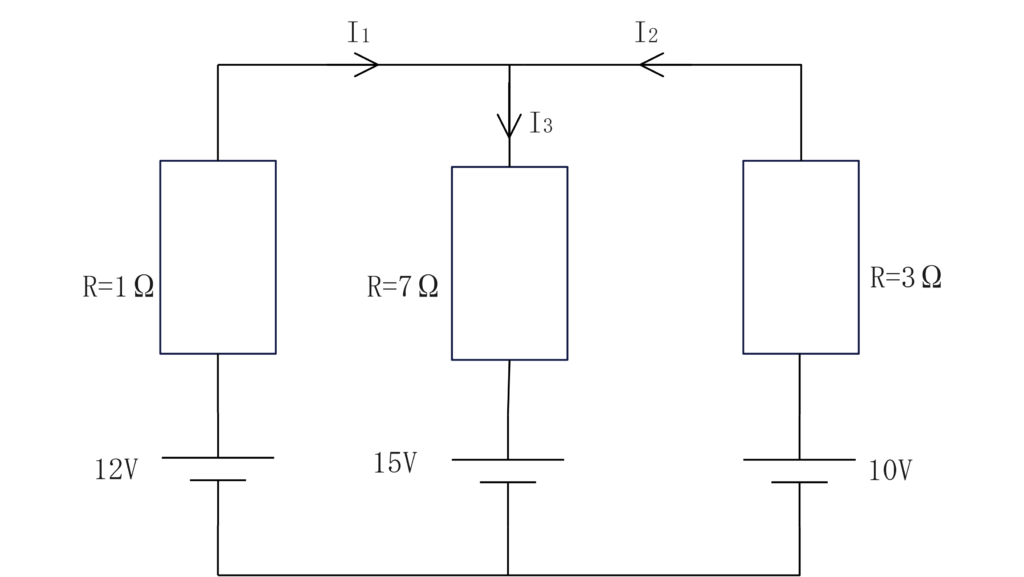
\(12-15=I_1+7I_3…①\)
\(10-15=3I_2+7I_3…②\)
\(I_1+I_2=I_3…③\)
③を➀、②に代入すると
\(-3=I_1+7(I_1+I_2)\)
\(-5=3I_2+7(I_1+I_2)\)
\(-3=8I_1+7I_2…④\)
\(-5=7I_1+10I_2…⑤\)
④×10-⑤×7より
\(-30=80I_1+70I_2\)
\(-35=49I_1+70I_2\)
\(31I_1=-5\)
\(I_1=-\frac{5}{31}\)
\(-3=\frac{40}{31}+7I_2\)
\(7I_2=-\frac{133}{31}\)
\(I_2=-\frac{19}{31}\)
③より
\(I_3=\frac{14}{31}\)
このようにキルヒホッフの法則を用いれば回路の電流を知ることができます。
また、電流がわかっている場合は電圧や抵抗を求めるなど様々な場面でキルヒホッフの法則を使うことができます。

コメント