今回は以下の回路のとき抵抗Rで消費(取り出)される電力Pが最大となる条件を考えていきます。
この条件を求める方法はいくつもありますが、今回は3つ紹介します。
まず、電力Pは\(P=VI=RI^{2}\)=\(\frac{V^{2}}{R}\)となります。
電圧源をE、内部抵抗をr、負荷抵抗をRとして以下の回路について考えていきます。
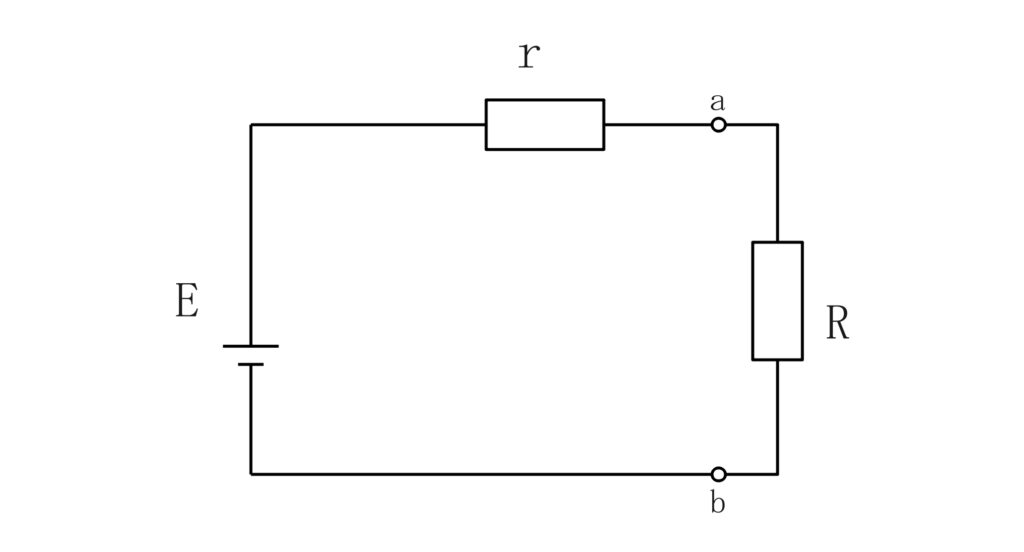
最小の定理を用いた方法
まず、負荷Rにかかる電圧VRをとすると、分圧則より
VR = \( \frac{R}{R+r}× E \)
Rで消費される電力PRは
PR=\(\frac{V_{R}^{2}}{R}\)=\(\frac{(\frac{R}{R+r}×E)^{2}}{R}\)=\(\frac{RE^{2}}{(R+r)^{2}}\)=\(\frac{RE^{2}}{R^{2}+2Rr+r^{2}}\)・・・(1-1)
上の式をRで割るとPR=\(\frac{E^{2}}{R+2r+\frac{r^{2}}{R}}\)となります。
分母が最小になるときPRは最大になります。
ここで、rは常に一定であり、Rが可変であるため分母で可変するのはRと\(\frac{r^{2}}{R}\)だけです。
最小定理より\(R×\frac{r^{2}}{R}=r^{2}\)より定数となるので\(R=\frac{r^{2}}{R}\)
よって、R2=r2 R=rのとき電力が最大となります。
最大となる電力Pmaxは(1-1)より
Pmax=\(\frac{E^{2}}{R+2r+\frac{r^{2}}{R}}\)=\(\frac{E^{2}}{R+2R+\frac{R^{2}}{R}}\)=\(\frac{E^{2}}{4R}\)[W]となります。
微分を用いた方法
(1-1)よりPR=\(\frac{RE^{2}}{(R+r)^{2}}\)この時この関数でRに対する傾きがゼロになるとき最大になるので
\(\frac{dP}{dR}\)=0より\(\frac{dP}{dR}\)=\(\frac{d}{dR}(\frac{RE^{2}}{(R+r)^{2}})\)=\(\frac{rE^{2}-RE^{2}}{(R+r)^{2}}\)=0
これがゼロとなるには分子が0になればいいため\(E^{2}\)でくくると\(E^{2}(r-R)\)=0
よって、R=rのとき電力が最大であるとわかる。
Pmax=\(\frac{E^{2}}{R+2r+\frac{r^{2}}{R}}\)=\(\frac{E^{2}}{R+2R+\frac{R^{2}}{R}}\)=\(\frac{E^{2}}{4R}\)[W]となります。
テブナンの定理
まず、負荷Rを外し、a-b間を開放します。そして、電源を短絡します。
a-b間の抵抗R0=r
a-b間の電圧Vab=E
よって、元の回路のa-b間に流れる電流は
\(I=\frac{V_{ab}}{R_0}\)=\(\frac{E}{r+R}\)となります。
よって、負荷Rで消費される電力PRは
\(P_R\)=\(RI^{2}\)=R\(\frac{E^{2}}{(r+R)^2}\)=\(\frac{E^{2}}{\frac{r^{2}}{R}+2r+R^{2}}\)
ここで最小の定理を用いるとR=rとなり
\(P_{max}\)=\(\frac{E^{2}}{4R}\)
また、最大消費電力の際の回路に流れる電流は\(I\)=\(\frac{E}{2R}\)
回路が並列の時
負荷Rに対して並列に抵抗が接続されているときの負荷の最大消費電力について求めていきます。
ます、以下の回路について考えます。
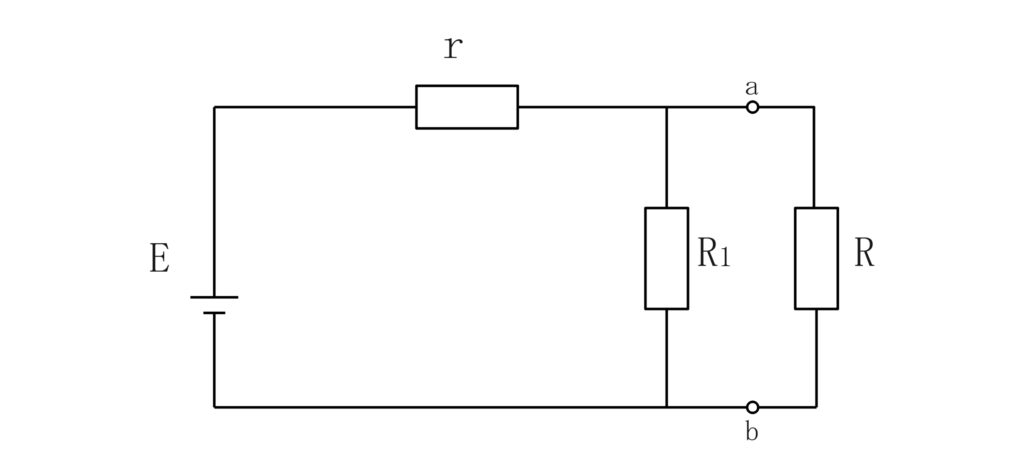
今回はテブナンの定理を用いて導いていきます。
まず、a-b間を開放、電源Eを短絡して合成抵抗R0を求めます。
\(R_0=\frac{rR_1}{r+R_1}\)
また、a-b間の電圧\(V_{ab}\)=\(\frac{R_1}{r+R_1}・E\)
負荷Rを接続したときに回路に流れる電流Iは
\(I=\frac{V_{ab}}{R+R_0}\)
よって、負荷R0で消費される電力P0は
\(P_0\)=\(R_0I^{2}\)=R_0\(\frac{V_{ab}^{2}}{(R+R_0)^2}\)=\(\frac{V_{ab}^{2}}{\frac{R_0^{2}}{R}+2R_0+R}\)
よって、\(P_{0max}\)=\(\frac{V_{ab}}{4R_0}\)
つまり、並列の場合であっても負荷での最大消費電力は負荷にかかる電圧を4倍の負荷抵抗で割った値になります。
まとめ
負荷にかかる電圧をV、負荷抵抗をRとすると、
常に、負荷Rにかかる最大消費電力Pは\(P=\frac{V^{2}}{4R}\)となります。



コメント