今回は直流回路と交流回路の違いについて説明していきます。
直流回路
まず、直流回路とは時間によって大きさと向きが周期的に変わらないもののことです。
直流回路における電圧源は以下のような記号で表されます。

直流回路でのオームの法則はV=IRが成り立ちます。
電圧と電流の変化
直流回路での時間と電圧、電流の変化は以下の図のようになります。
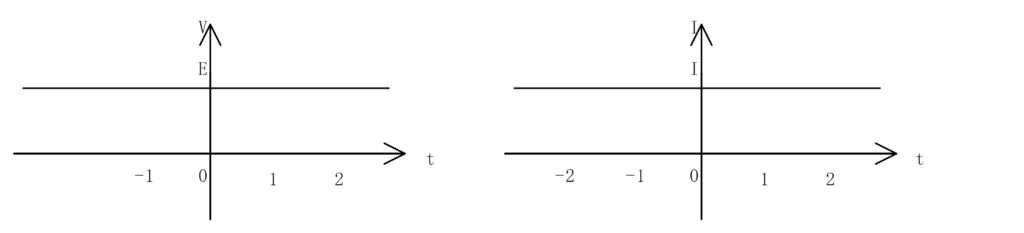
このように直流回路では時間によって変化が起こらないことがわかります。
用途
直流は乾電池やリチウム電池などから供給され、バッテリーの駆動機器、電子回路、LED照明、懐中電灯、パソコンなどに使用されています。
パソコンやスマホなどの充電にはAC/DCコンバータ(交流から直流にするもの)により直流が使われています。
動作する素子
電気回路では抵抗、コイル(インダクタンス)、コンデンサ(キャパシタ)以外にも様々な素子がありますが今回はこの3つについてふれていきます。
まず、抵抗はこれまで扱ってきたようにオームの法則から直流で使用することができます。
コイルは、v(t)=\(L\frac{di(t)}{dt}\)で表されます。
直流回路では電流値は常に一定なのでdi(t)は定数になります。
定数を微分するとゼロとなるためコイルにかかる電圧v(t)は0となります。
つまり、直流回路では導線(短絡)として扱うことができます。
コンデンサは、v(t)=\(\frac{1}{C}\int i(t)dt\)で表されます。
これを、i(t)表すとi(t)=\(\frac{dv(t)}{dt}・C\)となります。
直流回路では電圧は一定なのでコンデンサに流れる電流i(t)は0になります。
つまり、直流回路ではコンデンサは開放として扱うことができます。
交流回路
交流回路では時間により大きさと向きが変わります。
交流回路における電圧源は以下のような記号で表されます。
交流回路ではオームの法則が V=ZIとなります。
電圧と電流の変化
交流回路での時間と電圧、電流の変化は以下の図のようになります。

このように時間が変化するにつれ電圧、電流値は変化します。
用途
交流は家庭の電球やドヤイヤー、電子レンジなどの家電、産業用機器の電源などに使用されています。
動作する素子
まず、抵抗では直流回路と同様にオームの法則が成り立ちます。
これはv(t)=R・i(t)と表されます。
コイルでは、v(t)=\(L\frac{di(t)}{dt}\)で表されます。
交流回路ではi(t),v(t)はsinもしくはcos関数で表されるのでdtで微分するとsinもしくはcosとなります。
電流の最大値(振幅)をImとすると、
i(t)=Imsin(ωt+θ)の場合はv(t)=Imcos(ωt+θ)=ωImsin(ωt++θ+\(\frac{π}{2}\))、
i(t)=Imcos(ωt+θ)の場合はv(t)=-Imsin(ωt+θ)=ωImcos(ωt+θ+\(\frac{π}{2}\))となり
コイルでは電圧vが電流iに比べて\(\frac{π}{2}\)位相進みになることがわかります。
コンデンサでは、v(t)=\(\frac{1}{C}\int i(t)dt\)で表されます。
上の式を変形させるとi(t)=C\(\frac{dv(t)}{dt}\)
電圧の最大値(振幅)をVmとすると、
v(t)=Vmsin(ωt+θ)の場合はi(t)=CVmsin(ωt+θ)\(\frac{d}{dt}\)=CVmcos(ωt+θ)=CVmsin(ωt+θ+\(\frac{π}{2}\))
v(t)=Vmsin(ωt+θ)の場合はi(t)=CVmcos(ωt+θ)\(\frac{d}{dt}\)=-CVmsin(ωt+θ)=CVmcos(ωt+θ+\(\frac{π}{2}\))となり
コンデンサでは電流iが電圧vに比べて\(\frac{π}{2}\)位相進みになることがわかります。
まとめ
直流で動作するのはRのみ。Lは短絡、Cは開放される。
交流ではR、L、Cはそれぞれ動作します。
またLでは電圧は電流に比べて\(\frac{π}{2}\)位相進み、
Cでは電圧は電流に比べて\(\frac{π}{2}\)位相遅れとなります。



コメント