電圧計と電流計の内部抵抗についてわかりやすく解説

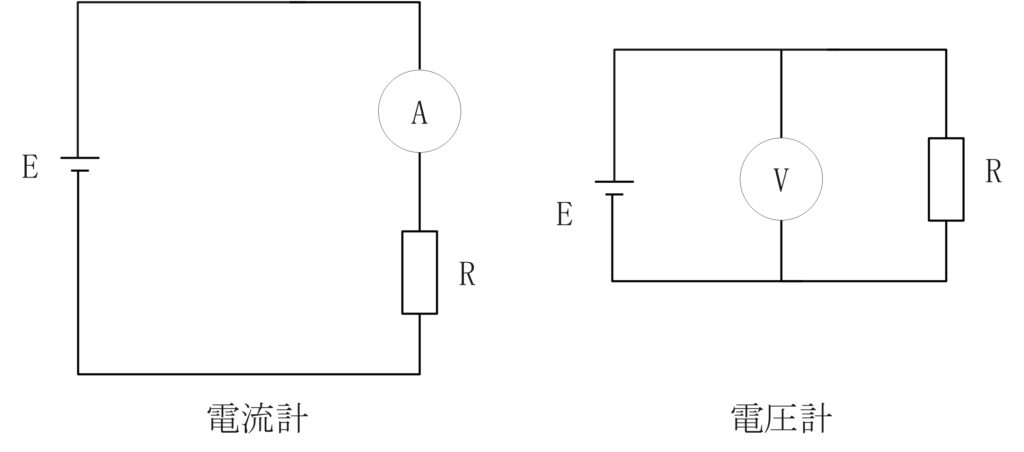
電流計、電圧計は下のような図記号を使用します。

電圧計と電流計の内部には抵抗が存在します。

その抵抗のことを内部抵抗といいます。

電流計は測りたいものに対して直列に、電圧計は測りたいものに対して並列に接続します。

電流計は内部抵抗が小さいため直列に接続しても全体の電流にほとんど影響しないためです。

電圧計は内部抵抗が大きいため並列に接続すると、測りたいものの電圧がほとんど等しくなるためです。

電流計や電圧計を回路に挿入する場合、以下のように回路図を組み立てます。

電流計の内部抵抗

以下の回路図を考えたとき内部抵抗の値が大きい場合と小さい場合について考えていきます。

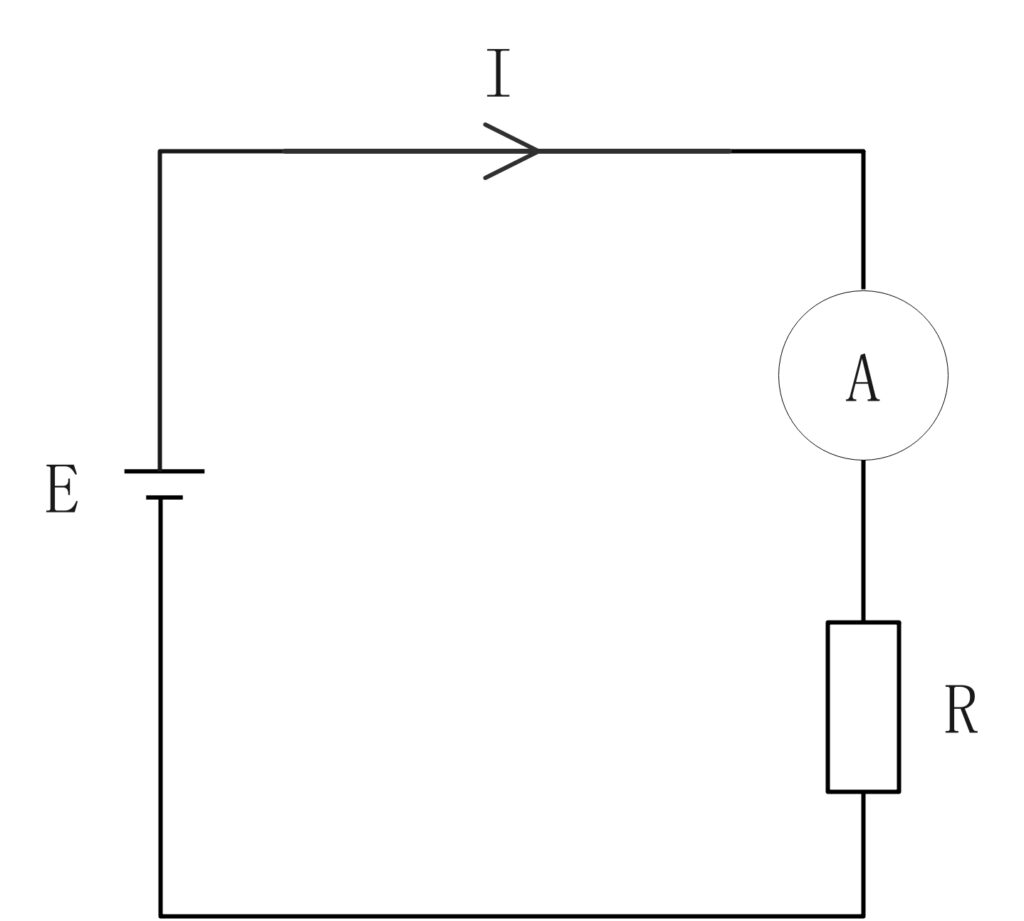
まず、オームの法則より回路全体の電流Iは、

I=\(\frac{E}{R+r}\)・・・(1-1)となります。　　R:抵抗　r:電流計の内部抵抗

内部抵抗を無視した時の電流値Iは

I=\(\frac{E}{R}\)・・・(1-2)となります。

r>>Rとすると、測りたい回路全体の電流値IがI=\(\frac{E}{R+r}\)より電流Iがほぼ０になってしまいます。

r<<Rとすると、測りたい回路全体の電流値IがI=\(\frac{E}{R+r}\)より

I=\(\frac{E}{R + r} \approx \frac{E}{R}\)と考えることができます。

以上より、内部抵抗の抵抗値rが大きい場合と小さい場合を比較すると、

電流計の内部抵抗を小さくする方が真値に近い電流値を負荷Rにかけることができます。

また、実際の電流計では内部抵抗は数Ω～数百Ω程度です。

以下の回路図を考えたとき内部抵抗の値が大きい場合と小さい場合について考えていきます。

まず、電圧は並列の場合等しくなるので負荷Rと電圧計の内部抵抗rにかかる電圧を等しくするために電圧計を並列に接続します。

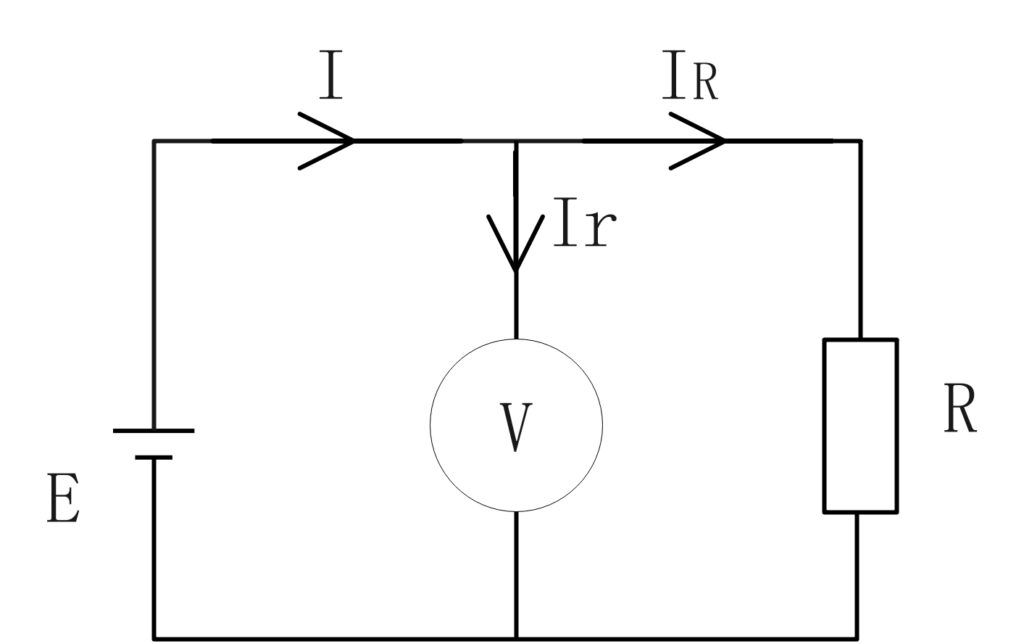
まず、電圧計にかかる電流Irと負荷Rにかかる電流I_Rはそれぞれ

I_R=\(\frac{r}{R+r}・I\)

Ir=\(\frac{R}{R+r}・I\)となります。 R:負荷 r:電圧計の内部抵抗

次に内部抵抗が大きい場合と小さい場合どちらがよいか考えていきます。

r<<Rとすると

I_R=\(\frac{r}{R+r}・I \approx \frac{I}{R}\)

Ir=\(\frac{R}{R+r}・I \approx \frac{R}{R}・I=I\)

となり、電圧計にほとんどの電流が流れてしまいます。

r>>Rとすると

I_R=\(\frac{r}{R+r}・I \approx \frac{r}{r}・I=I\)

Ir=\(\frac{R}{R+r}・I \approx 0\)

となり、負荷Rにほとんどの電流を流すことができます。

以上より、内部抵抗の抵抗値rが大きい場合と小さい場合を比較すると、

大きい場合のほうがRに回路全体のほとんどの電流を流すことができます。

実際の電圧計では内部抵抗は数メガΩ程度です。

電流計は内部抵抗の小さいものほど真値に近い電流を流すことができます。

電圧計は内部抵抗の大きいものほど真値に近い電流を流すことができます。

つまり、電流計は内部抵抗の小さいもの、電圧計は内部抵抗の大きいものほど精度のよいものといえます。