分圧の法則、分流の法則をわかりやすく解説

直列回路と並列回路では、流れる電流と電圧が変わってきます。

今回は分流の法則と分圧の法則について説明していきます。

・分圧の法則とは
・分流の法則
まとめ

・分圧の法則とは

直列回路では負荷にかかる電圧はそれぞれ変化します。

このような時に負荷にかかる電圧値を求めるために分圧の法則が使用されます。

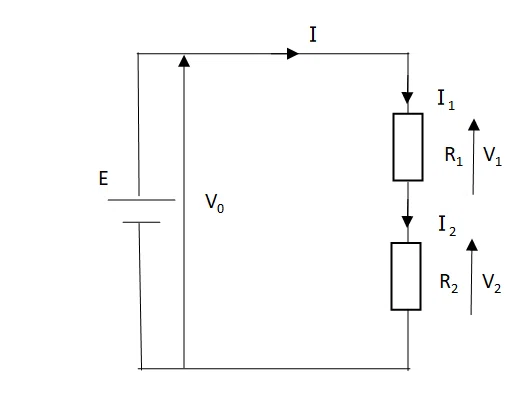
まず、下の回路について考えていきます。

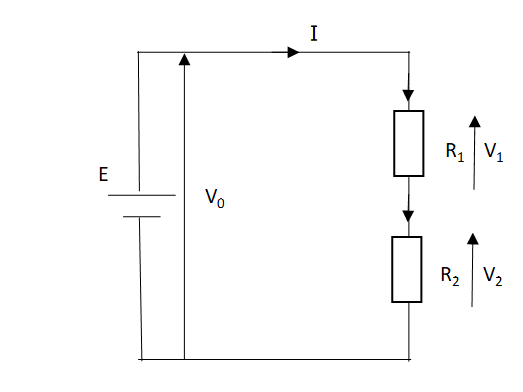
この回路の合成電圧は　V₀=V₁+V₂　・・・(1-1)
　　　　　合成抵抗は　R₀=R₁+R₂

抵抗R1にかかる電圧V1は　V₁=R₁・I　・・・(1-2)
抵抗R2にかかる電圧V1は　V₂=R₂・I　・・・(1-3)

(1-1)、(1-2)、(1-3)より

V₀=R₁・I+R₂・I=(R₁+R₂)・I

\( I = \frac{V_0}{R_1 + R_2} \) ・・・(1-4)

(1-4)を(1-2)、(1-3)に代入すると

V₁=\(\frac{R_1}{R_1+R_2}・V_0\)

V₂=\(\frac{R_2}{R_1+R_2}・V_0\)

この式を利用して解けば分圧を求めることができる。

・例題(抵抗二つ)

R₁にかかる電圧をV₁、R₂にかかる電圧をV₂を求める。

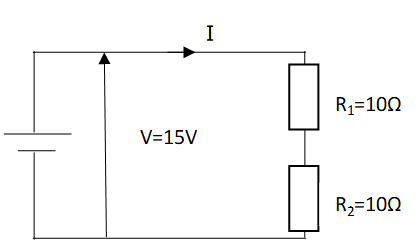
V₁=\(\frac{R_1}{R_1+R_2}・V_0\)=\(\frac{10}{10+10}・15\)=7.5[V]
V₂=\(\frac{R_2}{R_1+R_2}・V_0\)=\(\frac{10}{10+10}・15\)=7.5[V]

検算をしてみるとこの直列回路の合成電圧はV=V1+V2で求められる。
　　　　　　V=7.5+7.5=15[V]
よって、間違がないことがわかります。

・抵抗が3つ以上の場合

この回路の合成電圧は　V₀=V₁+V₂・・・V_n　・・・(2-1)
　　　　　合成抵抗は　R₀=R₁+R₂+R_n

抵抗R1にかかる電圧V1は　V₁=R₁・I　・・・(2-2)
抵抗R1にかかる電圧V1は　V₂=R₂・I　・・・(2-3)
・
・
・
　　　　　　　　　　　　 V_n=R_n・I　・・・(2-4)

(2-1)、(2-2)、(2-3)、(2-49より
V₀=R₁・I+R₂・I +・・・+R_n・I=(R₁+R₂+・・・+R_n)・I
I=\(\frac{V_0}{R_1+R_2+・・・+Rn}\) ・・・(1-4)

(1-4)を(1-2)、(1-3)に代入すると
V₁=\(\frac{R_1}{R_1+R_2+・・・+R_n}・V_0\)
V₂=\(\frac{R_2}{R_1+R_2+・・・+R_n}・V_0\)

・例題（抵抗三つ)

R₁=100[Ω]、R₂=200[Ω]、R₃=300[Ω]、E=10[V]とする。
電圧V₁、V₂、V₃を求める。

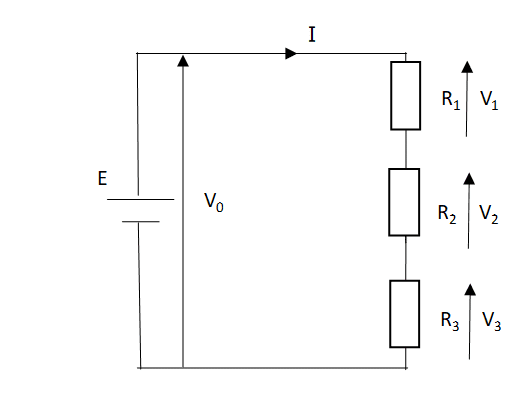
V₁=\(\frac{R_1}{R_1+R_2+R_3}・E\)=\(\frac{100}{100+200+300}・10\)=\(\frac{5}{3}\)[V]
V₂=\(\frac{R_2}{R_1+R_2+R_3}・E\)\(\frac{200}{100+200+300}・10\)=\(\frac{10}{3}\)[V]
V₁=\(\frac{R_3}{R_1+R_2+R_3}・E\)=\(\frac{300}{100+200+300}・10\)=5[V]

・覚え方

　　　　求めたい電圧＝\(\frac{求めたい電圧の抵抗}{合成抵抗}・全体の電圧\)

・分流の法則

並列回路において電流はそれぞれの抵抗に分かれます。
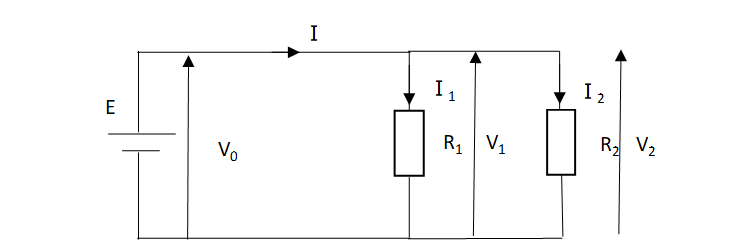
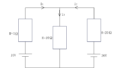
以下のような抵抗が並列接続された回路を考える。

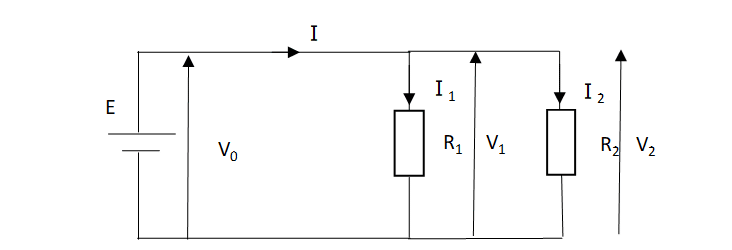
この回路の合成抵抗は　R₀=\(\frac{R_1・R_2}{R_1+R_2}\) ・・・(3-1)
この回路は並列接続であるため電圧は等しくなる。
　　　　　　　　　　　V₀=V₁=V₂
電圧V0は　V₀=R₀・I　より
R₁・I₁＝R₀・I　・・・(3-2)
R₂・I₂＝R₀・I　・・・(3-3)

ここで、(3-1)を(3-2)、(3-3)に代入すると
R₁・I₁=\(\frac{R_1・R_2}{R_1+R_2}・I\)
I₁について解くとI₁＝\(\frac{R_2}{R_1+R_2}・I\)
R₂・I₂=\(\frac{R_1・R_2}{R_1+R_2}・I\)
I₂について解くとI₂=\(\frac{R_1}{R_1+R_2}・I\)

・例題(抵抗二つ)

R₁に流れる電流I₁、R₂に流れる電流I₂を求める。
R₁=100[Ω]、R₂=200[Ω]、I=3[A]とする。

I₁=\(\frac{R_2}{R_1+R_2}・I\)=\(\frac{100}{100+200}・3\)=1[A]
I₂=\(\frac{R_1}{R_1+R_2}・I\)=\(\frac{200}{100+200}・3\)=2[A]

検算をしてみるとこの並列回路の合成電圧はI=I₁+I₂で求められる。
　　　　　　I=1+2=3[A]
よって、間違がないことがわかる。

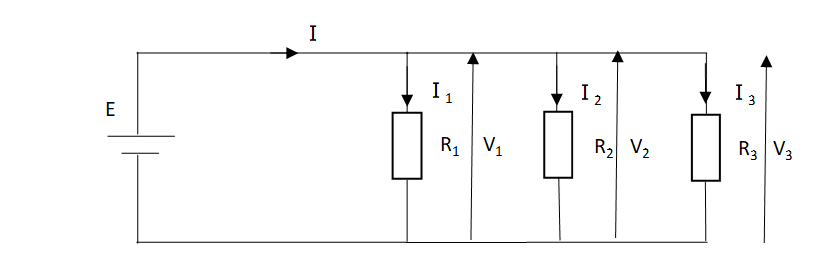
・抵抗が３つ以上の場合

この回路の合成抵抗は　R₀＝\(\frac{1}{G_1+G_2+・・・+G_n}\)　・・・(3-1)
この回路は並列接続であるため電圧は等しくなる。
　　　　　　　　　　　V₀=V₁=V₂=V_n
電圧V₀は　V₀=R₀・I　より
R₁・I₁＝R₀・I　・・・(3-2)
R₂・I₂＝R₀・I　・・・(3-3)
・
・
R_n・I_n＝R₀・I　・・・(3-4)

ここで、(3-1)を(3-2)、(3-3)、(3-4)に代入すると
R₁・I₁=\(\frac{1}{G_1+G_2+・・・+G_n}・I\)
I₁について解くとI₁＝\(\frac{G_1}{G_1+G_2+・・・+G_n}・I\)
R₂・I₂=\(\frac{1}{G_1+G_2+・・・+G_n}・I\)
I₂について解くとI₂=\(\frac{G_2}{G_1+G_2+・・・+G_n}・I\)
R_n・I_n=\(\frac{1}{G_1+G_2+・・・+G_n}・I\)
I_nについて解くとI_n＝\(\frac{G_n}{G_1+G_2+・・・+G_n}・I\)