キルヒホッフの法則は、ドイツの物理学者グスタフ・キルヒホフによって導きだされました。キルヒホッフの法則は二つの公式があります。
第一法則
回路中の任意の接続点に流入出する電流の和は0である。
これは下図のように節点に対して、流れ入る電流を(+)、流れでる電流を(-)としたときにその和が常に0になるということである。
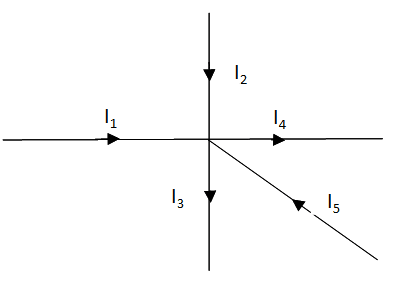
式にして表すと、 I1+I2-I3-I4+I5=0
これを書き換えると I1+I2+I5=I3+I4
つまり、流れ出る電流と入る電流は等しいということです。
第二法則
回路中の任意の閉路を一周するとき、起電力の総和と電圧降下の総和は等しい。
まず、閉路とは始点と終点の位置が同じであることに等しい。
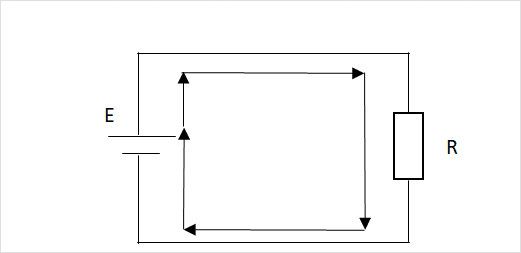
下図の回路ではEを始点としてみると、Eが終点となるよう矢印のように一周したもののことである。
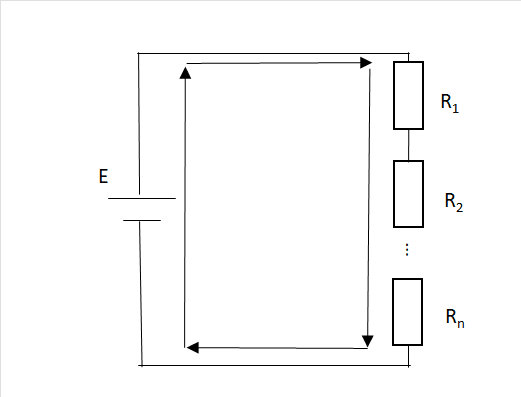
下図の回路においてR1からRnまでで消費される電圧の和は起電力Eと同じになります。
つまり、E=(R1+R2+・・・Rn)・Iとなります。
一般的に第一法則をKCL(Kirchhoff’s Current Low)
第二法則をKVL(Kirchhoff’s Voltage Low)といいます。
例題
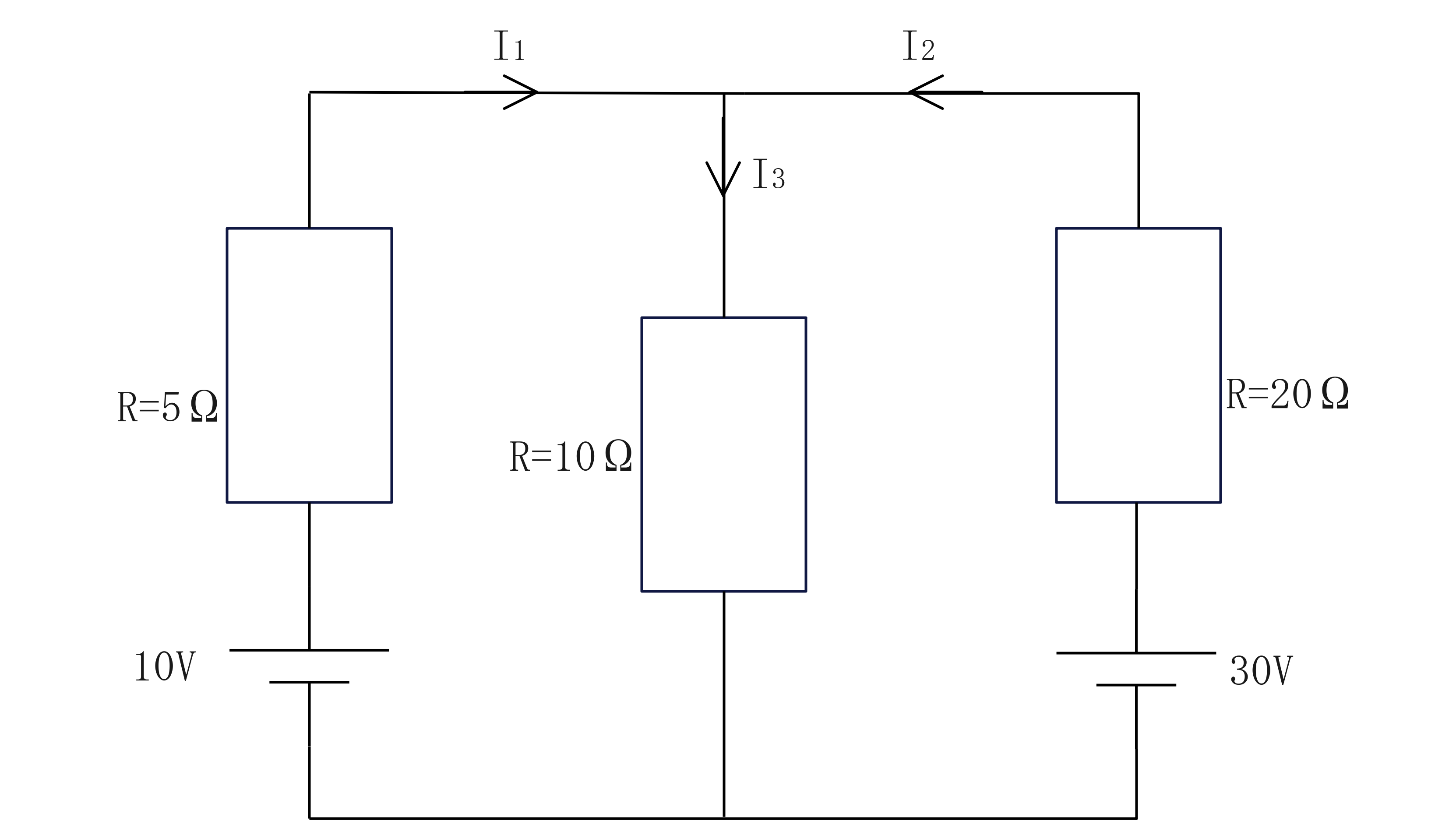
下図においてI1、I2、I3を求める。
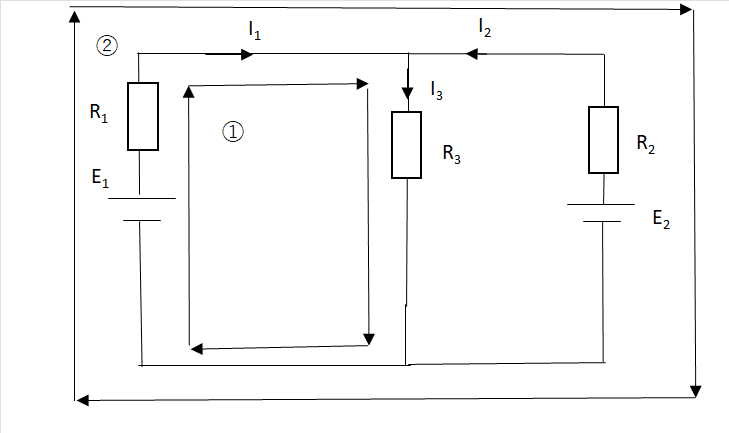
連立方程式による解き方
キルヒホッフの法則を用いてI1、I2を求める。
ここで、E1=15V、E2=10V、R1=10Ω、R2=20Ω、R3=30Ωとします。
まず、KCLを適応します。
R3に流れる電流をI3とすると、
I3=I1+I2・・・(1-1)
次にKVLを適応します。
R3に流れる電流をI3とすると、
閉路①: E1=R1・I1+R3・I3
15=10・I1+30・I3・・・(1-2)
閉路②: E1-E2=R1・I1-R2・I2
15-10=10・I1-20・I2・・・(1-3)
(1-2)に(1-1)を代入すると、
15=10・I1+30(I1+I2)・・・(1-4)
(1-4)・2+(1-3)・3より
110・I1=45
\(I_1=\frac{45}{110}=\frac{9}{22}\)
15=40・\(\frac{9}{22}\)+30・\(I_2\)
(1-4)より
30・\(I_2\)=\(-\frac{180}{11}+\frac{165}{11}\)
\(I_2=-\frac{1}{22}\)
(1-1)より
\(I3=\frac{9}{22}-\frac{1}{22}=\frac{8}{22}=\frac{4}{11}\)
以上のようにI1、I2、I3を求めることができます。
実際に、以上で求めた電流があっているかを求めるには
(1-2)、(1-3)に求めた電流を代入すれば確認することができます。
まとめ
キルヒホッフの法則は閉回路を作り連立方程式を作ることにより素子の値を求めることができます。

コメント